Path Planning With TWTLPlan

Motion planning is a fundamental problem in robotics. The objective is to generate control policies for a robot to drive it from an initial state to a goal region in its state space under kino-dynamic constraints Even without considering dynamics, the problem becomes increasingly difficult in high dimensions, and it has been shown to be PSPACE-complete. A class of algorithms was developed relying on randomly sampling the configuration space of the robot and planning local motions between these samples. Probabilistic Roadmaps and Rapidly Exploring Random Trees are among the most widely known examples, along with their asymptotically optimal variants, PRM$^*$ and RRT$^*$.

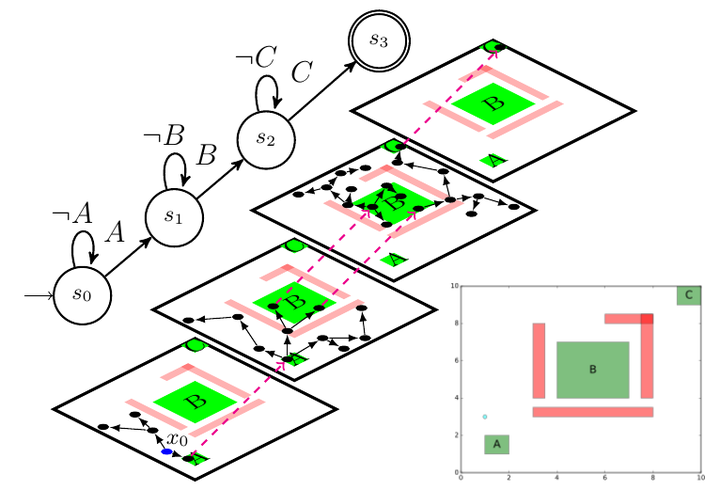
Robots are increasingly required to perform complex tasks, where correctness guarantees, such as safety and liveness in human-robot teams and autonomous driving, are critical. One approach is to encode the tasks as temporal logic specifications and leverage formal methods techniques to generate control policies that are correct by construction. As opposed to traditional methods restricted to reach-avoid setups, these frameworks are able to express more complex tasks such as sequencing (e.g., “Reach $A$, then $B$"), convergence (“Go to $A$ and stay there forever”), persistent surveillance (“Visit $A$, $B$, and $C$ infinitely often”), and more complex combinations of the above. Some applications additionally require time constraints. For example, consider the following task: “Visit $A$, $B$, and $C$ in this order. Perform action $a$ for 2 time units at $A$ within 10 time units. Then, perform $b$ for 3 time units at $B$ within 6 time units. Finally, in the time window $[3, 9]$ after $b$ is finished, perform $c$ for 1 time unit at $C$. All three actions must be finished within 15 time units.” Temporal logics such as Linear Temporal Logic (LTL) or Computational Tree Logic (CTL) can be used to encode the former kind of tasks, while tasks with explicit time constraints may be expressed using bounded linear temporal logic (BLTL), metric temporal logic (MTL), signal temporal logic (STL), and time-window temporal logic (TWTL).

A natural approach to generate control strategies from rich task specifications for robots with large state spaces is to combine sampling-based techniques with automata-based synthesis methods. In this project, we proposed a language-guided sampling-based method to generate robot control policies satisfying tasks expressed as TWTL formulae. A TWTL formula formally captures the notion of performing tasks of a certain duration in regions of interest in order. For example, a specification in natural language such as “perform task A of duration 1 within 2 time units; then, within the time interval [1, 8] perform tasks B and C of durations 3 and 2, respectively; furthermore, C must be finished within 4 time units from the start of B;” would correspond to the following TWTL formula:

$$ f = [H^1 A]^{[0, 2]} * [H^3 B \wedge [H^2 C]^{[0, 4]}]^{[1, 8]} $$

A key feature of TWTL is that a formula may be relaxed, i.e., we can add a variable delay to each deadline. A relaxed formula with a positive delay is a weaker specification, while a negative delay indicates a stronger specification. A path satisfying a stronger specification satisfies a weaker one. TWTLPlan makes use of this feature by finding a path that satisfies a weaker specification first, then attempts to reduce the delay until the original specification is satified. These paths are computed using a sampling-based algorithm called RRT$^*$.

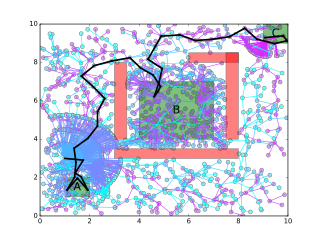
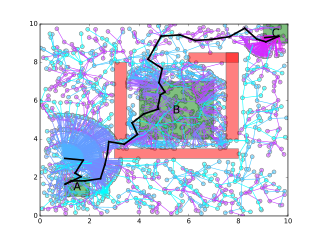
This approach has two advantages: (a) the growth of the sampling graph is biased towards satisfaction of a relaxed version of the specification without initially taking into account deadlines, and (b) after an initial policy has been found, sampling can be focused on the parts of the plan that need to be improved. The two stages can be thought of as exploration-exploitation phases, where initially candidate solutions are found, and then focused local sampling is performed on the parts that need to be improved in order to satisfy the specification, i.e. time constraints. As a byproduct, a satisfying policy with respect to a minimally relaxed version of the specification may be returned when the original problem does not have a solution. Such a policy may inform operators about timing problems in the specification or system (i.e., robot dynamics and/or environment). The algorithm uses annotated finite state automata to represent all possible temporal relaxations of a TWTL formulae. We were also able to prove that our solution is probabilistically complete.

We implemented our path planning algorithm in TWTLPlan. Using this tool you can define 2D scenarios with rectangular obstacles and regions of interest and generate satisfying paths for specifications given in a subset of TWTL.